
В последнее время для морфометрических измерений в гидробиологии всё чаще используются возможности компьютерной 2D-графики. При этом, объекты данной предметной области, как правило, имеют неправильную форму, в отличие от объектов в других предметных областях, где имеют дело с геометрическими фигурами. Кроме этого, наблюдения и измерения зачастую делаются в полевых условиях, где невозможно использование стационарных (десктопных) компьютеров. Особый интерес в этой связи представляют возможности веб-технологий для использования в так называемых "облачных, web2" вычислениях.
Мы рассмотрим пример реализации (далее - пример) таких вычислений для расчёта площади и периметра сечений раковины двустворчатого моллюска по цифровым снимкам и измеренным ширине и высоте раковины (далее - веб-инструмент). Площадь, периметр и ошибки их расчёта рассчитываются, соответственно, вначале в пикселах, а затем - в квадратных миллиметрах и миллиметрах.
Реализация примера представляет собой веб-страницу с программами (скриптами) на стороне клиента, написанными на языке Javascript, с использованием свойств и методов программного интерфейса (API - application programming interface) HTML5 Canvas [1÷7].
Также, как и элемент HTML5 SVG [2], предназначенный для работы с векторной графикой, элемент HTML5 Canvas, более удобный для работы с растровой графикой, стал поддерживаться браузерами относительно недавно и, несмотря на бум посвящённых ему публикаций, примеров его применения в различных предметных областях ещё недостаточно. В то же время привлекает доступность и лёгкость использования свойств и методов этого элемента по сравнению с другими, более "тяжёлыми" технологиями (например, WebGL [8,9]).
Зачем необходимо исследование этих, казалось бы достаточно простых расчётов? В первую очередь из-за того, что фигуры и линии контуров этих фигур отображается не совсем одинаково в разных клиентах (браузерах). Поэтому немаловажно узнать о точности определения площади и периметра в зависмости от типа браузера. Кроме этого, возможна зависимость результатов от разрешения монитора, масштаба изображения (zoom) и разрешения снимка.
Данный пример позволяет выполнить эксперименты с веб-инструментами для определения точности расчёта площади и периметра фигур разных размеров, помещаемых в HTML5 Canvas, с использованием различных браузеров и мониторов.
Результаты таких экспериментов позволяют сделать выводы о применимости предлагаемых веб-инструментов.
Итак, цель доклада: проиллюстрировать возможности использования новых технологий, а именно, API HTML5 Canvas, в практике будущего гидробиолога-морфометриста.
Основная задача состоит в построении тестовой геометрической фигуры средствами API HTML5 Canvas с использованием языка Javascript и в приближённом вычислении площади и периметра этой фигуры по её растровому представлению. В качестве такой фигуры взят эллипс. Точную величину площади эллипса можно определить по аналитической формуле. Периметр эллипса будем определять по формуле Рамануджана (приближённой, но для нашей задачи будем считать её точной).
Сравнение приближённых и точных значений позволяет вычислить абсолютные и относительные ошибки определения площади и периметра фигуры по её растровому изображению.
Поскольку на эллипс похожи формы сечений раковин некоторых двустворчатых моллюсков, то полученные результаты можно по аналогии распространить на измерения реальных раковин.
Окончательное подтверждение возможности использования предлагаемых "веб-инструментов" проверим на опытных экземплярах раковин черноморских мидий.
Итак, перечислим этапы, которые нам необходимо пройти.
Задаём: ширину и высоту эллипса (в пикселах).
Выполняем: 1) рисуем и закрашиваем эллипс; 2) рассчитываем площадь, периметр и ошибки их расчёта (в пикселах).
Задаём: прямоугольное изображение с эллипсом, полученное на первом этапе.
Выполняем: 1) выделяем растровую фигуру на изображении; 2) рассчитываем площадь, периметр и ошибки расчёта (в пикселах).
Задаём: 1) прямоугольное изображение с эллипсом, полученное на первом этапе; 2) длину и ширину эллипса на изображении и ошибку их измерения (в мм).
Выполняем: 1) выделяем растровую фигуру на изображении; 2) рассчитываем площадь, периметр и ошибки расчёта с учётом ошибок измерения (в мм).
Задаём: 1) фото раковины; 2) длину, ширину и ошибку их измерения (в мм).
Выполняем: 1) выделяем растровую фигуру раковины; 2) рассчитываем площадь, периметр и ошибки расчёта с учётом ошибок измерения (в мм).
Более полное представление о каждом из перечисленных этапов можно получить, перейдя к действующему примеру.
Вначале немного об эллипсе, который используется в качестве модели изображения раковины.
Напомним, что на первом этапе мы используем холст с предварительно нарисованным и закрашенным контуром эллипса, а на последующих двух этапах берём прямоугольную картинку (растровое изображение) с этого холста. На этой картинке контур нарисованной ранее фигуры надо каким-то образом снова выделить. При выделении контура по растровому изображению неизбежно вносится какая-то дополнительная ошибка.
Это надо знать, потому что на первом этапе, используя фигуру сразу после прорисовки её контура, мы можем облегчить свою задачу, используя встроенный метод cntxt.isPointInPath(i,j), предусмотренный для проверки, находится ли точка (пиксел) с координатами (i,j) внутри контура. Мы, таким образом, не вносим дополнительной ошибки, связанной с необходимостью определения местоположения точек контура, как это происходит при работе с растровым изображением на последующих этапах. Более подробно об HTML5 Canvas и используемых свойствах и методах API для работы с ним можно узнать в Приложении и источниках из списка.
Площадь эллипса, как геометрической фигуры, вычисляется по известной формуле и это не требует пояснений.
Периметр геометрического эллипса будем вычислять по известной формуле Рамануджана, ошибка которой не превышает 0.02%.
По помещённому ниже коду функции, реализующей определение площади эллипса, представленном в растровом виде, также не трудно понять, как это делается.
Алгоритм расчёта периметра растровой фигуры более сложен. Ниже приведён код соответствующей функции.
Следует отметить, что предлагаемый алгоритм расчёта периметра является оригинальной разработкой, учитывающей особенности формы раковины черноморской мидии. По классификации алгоритмов выделения контуров [10] настоящий алгоритм следует отнести к сканирующим алгоритмам. С учётом типа исследуемых фигур использование алгоритмов этого типа представляется более оправданным, чем отслеживающих алгоритмов (или алгоритмов обхода контура, алгоритмов "жука").
Алгоритм включает два последовательно выполняемых блока. Вначале определяются крайние точки внешнего контура фигуры: левая, верхняя, правая и нижняя. Затем начинается проверка каждого пиксела на предмет его принадлежности фигуре: вначале от левой до верхней точки контура, затем от верхней до правой и так до замыкания контура.
Кратко о решении проблем, которые возникли при разработке этого алгоритма:
Порядок вычислительной сложности алгоритма (под сложностью будем понимать время, затрачиваемое на вычисления) удалось снизить не менее чем до величины ~O(N2/3) за счёт того, что просматривались лишь пиксели вокруг внешнего контура фигуры и не затрагивались точки внутри контура. Поскольку фигуры исследуемых объектов занимают обычно не менее трети холста (для эллипса - π/4), то в результате имеем указанную выше оценку вычислительной сложности. Под N можно понимать средние геометрические размеры фигуры. (Анастасии - о понятии "порядок вычислительной сложности алгоритма" хорошо сказано здесь)
Выпуклой называется такая фигура, которой принадлежат все точки отрезка, соединяющего любые ее две точки. Исследуемые фигуры раковин моллюсков не всегда являются выпуклыми. По этой причине просмотр (или сканирование) пикселей, например только лишь по горизонтали, может привести к неверным результататам. Для раковины мидии невыпуклость может появляться (а может и не появляться) примерно в одних и тех же местах или секторах при используемом нами методе поиска точек контура. Поэтому сектор с возможной невыпуклостью контура разбивается на два сектора и сканирование пикселей в этих "полусекторах" выполняется в разных направлениях. Многочисленные случаи проверки алгоритма на снимках реальных раковин не выявил ошибок при наличии невыпуклости.
Поскольку растровые фигуры имеют ступенчатый контур, то простой подсчёт пикселей контура не будет равен его длине, то есть периметру исходной фигуры. Определение длины вертикальных или горизонтальных линий в растре наиболее просто: проводится подсчёт числа пикселей, через которые проходит контур. Аналогично - для горизонтали. Но если линия ориентирована не точно по горизонтали или вертикали, такой метод не будет точным. Например, если линия проходит точно по диагоналям ячеек, то ее длина будет очевидно больше примерно в 1.414 раз, чем произведение разрешения на число ячеек. В настоящем алгоритме ступенчатый контур аппроксимируется ломанной линией. Конечно, это даёт возможность более точно определить длину контура отображаемой фигуры, но также с некоторой ошибкой, которую мы в последующем попытаемся определить.
Приведённый выше код функции по расчёту периметра относится к фигуре, нарисованной на первом этапе. Для определения принадлежности контуру фигуры, также как при расчёте площади, используется встроенный метод cntxt.isPointInPath(i,j), предусмотренный в API HTML5 Canvas для проверки, находится ли точка (пиксел) с координатами (i,j) внутри контура.
Завершая описание алгоритмов первого этапа напомним, что этот этап предназначен для экспериментов по определению оптимальных размеров растрового изображения для различных дисплеев и браузеров.
Полученные при этом результаты представлены в разделе 3 настоящего доклада.
На втором и последующих этапах нашего примера изображение вначале копируется с первого холста на другой холст, а затем контур фигуры выделяется фильтром на изображении. Таким образом, мы как-бы моделируем фотоснимки раковины, проверяя возможные результаты на тестовых фигурах.
Ниже приведена функция, предназначенная для копирования рисунка, получаемого на первом этапе.
Для копирования используется новая возможность HTML5 - поддержка интернет-адресов (или путей к файлу) типа dataURL (URL с данными-закодированными изображениями). То есть, такие адреса содержат не только пути (ссылки) к изображению, но сами изображения в закодированном виде (обычно Base64). Поэтому мы имеем возможность превратить содержимое холста в такой адрес с изображением (метод toDataURL("MIME-тип_изображения")), загрузить его в объект-изображение, не отображая это изображение, и затем загрузить и отобразить на холсте (метод drawImage(адрес_изображения, 0, 0)). Такая последовательность действий осуществляется с помощью операторов:
var srcImg = cnvs_in.toDataURL("image/png"); // Создаём dataURL, взяв изображение из первого холста
var img_ellips = new Image(); // Создаём элемент Image
img_ellips.src = srcImg; // и передаём ему путь к dataURL
img_ellips.onload = function() {
cntxt_out.drawImage(img_ellips, 0, 0); // Загружаем объект-изображение на нужный холст
}
Для выделения используется упрощённый вариант фильтра Собела [10,11]. Фильтр Собела по существу состоит в вычислении и анализе градиента перепада цветов. Упрощение заключается в том, что мы вычисляем лишь модуль градиента, без учёта направления. Такое упрощение оправдано тем, что мы имеем дело с предварительно обработанными изображениями (фон одного цвета), а само изображение обладает "гладким" и достаточно резко выделяющимся контуром. Тем не менее, без использования подобного фильтра обойтись не удаётся, поскольку на изображении могут быть участки, которые необходимо отфильтровать (кроме возможности обнаружения перепадов цвета, фильтр обладает сглаживающими свойствами).
Ниже приводится код функции по вычислению массива модулей градиента для выделения контура фигуры по Собелу.
Рассчитывается модуль градиента только лищь для одного, первого, цвета. В используемой цветовой rgba-модели - это красный цвет. Как показали эксперименты, фильтрации по одному цвету для нашей задачи оказалось достаточно. Функция возвращает двумерный массив модулей градиента, а для визуального контроля пиксели с модулями градиента, превышающими заданный порог, окрашиваются в зелёный цвет. Значение порога подобрано экспериментально.
Отличие в алгоритмах расчёта площади и периметра на третьем и четвёртом этапах состоит в необходимости учёта разрешения изображения фигуры в миллиметрах (количества миллиметров в пикселе) по горизонтали и по вертикали.
Первый этап можно использовать для определения того, как будут меняться ошибки определения площади и периметра в зависимости от типа используемых дисплея [12÷16] и браузера при изменении размера тестовой фигуры в пикселах. В качестве тестовой фигуры возьмём эллипс с соотношением сторон 2:1. При изменении размеров фигуры меняется разрешение изображения, от которого зависит точность определения площади и периметра. Последовательно увеличивая размер фигуры можно проследить изменение точности.
Для выполнения этой задачи студенты группы МК-1 собрали необходимую статистику, запуская наш пример и выполняя с его помощью расчёты первого этапа на имеющихся дисплеях в браузерах: Opera, Firefox, Safari и Chrome.
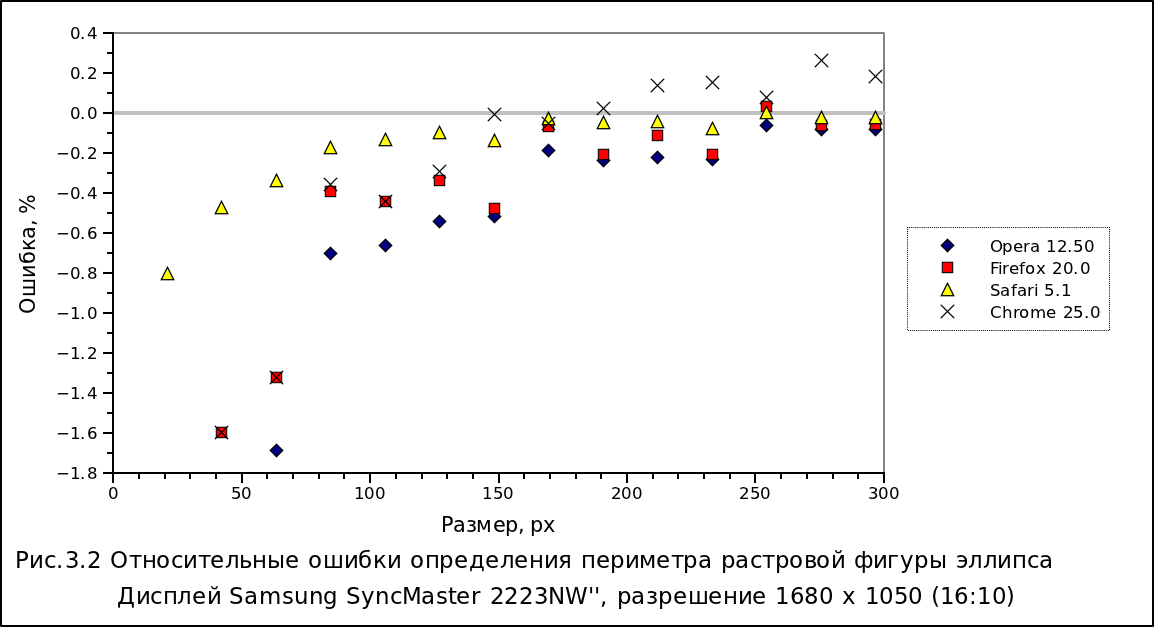
Некоторые результаты, типичные для всех использованных студентами десктопных дисплеев и ноутбуков, представлены на размещённых ниже графиках. По оси абсцисс отложены средние размеры фигуры (среднее геометрическое, в пикселах), по оси ординат - относительная ошибка расчёта площади или периметра (в процентах).


Ошибка определения площади и периметра для всех браузеров на различных типах мониторов [12÷16] снижается при увеличении размера изображения, но уже при размере более 170 пикселей ошибка уменьшается незначительно. На основании подобных экспериментов можно сделать вывод, что не имеет смысла делать снимки более 170 px, поскольку точность определения площади и периметра для снимков большего разрешения существенно не улучшится. В то же время небольшие размеры изображений позволят существенно уменьшить размер файлов базы данных для их хранения.
Следует отметить, что динамика и знак ошибок в Google Chrome заметно отличается от остальных браузеров. В этом браузере расчётные значения площади и периметра превышают истинные (ошибаемся в сторону увеличения площади и периметра) и при увеличении разрешения снимка остаются на достаточно большом уровне (около 0.3% для площади и 0.2% для периметра), тогда как для остальных браузеров ошибка приближается к нулю. Наилучшими показателями для нашей задачи обладает Safari.
Проводились также одиночные эксперименты со смартфонами и планшетами, работающие с браузерами Opera и Chrome. Предварительно можно сказать, что получаются аналогичные результаты, но величина ошибок колеблется для различных масштабов изображений, так как приходится использовать zoom.
Второй этап можно использовать для определения того, как будут меняться ошибки определения площади и периметра в зависимости от типа используемых дисплея и браузера и от размера изображения тестовой фигуры. В отличие от первого этапа эта фигура выделяется посредством фильтра и, конечно, каким-то образом искажается. Поэтому сделанные выше выводы для идеальной фигуры, неискажённой фильтрацией, требуют уточнения.
Результаты, экспериментов, аналогичных тем, которые проводились при использовании первого этапа, демонстрируются на рис.4.1 и 4.2.

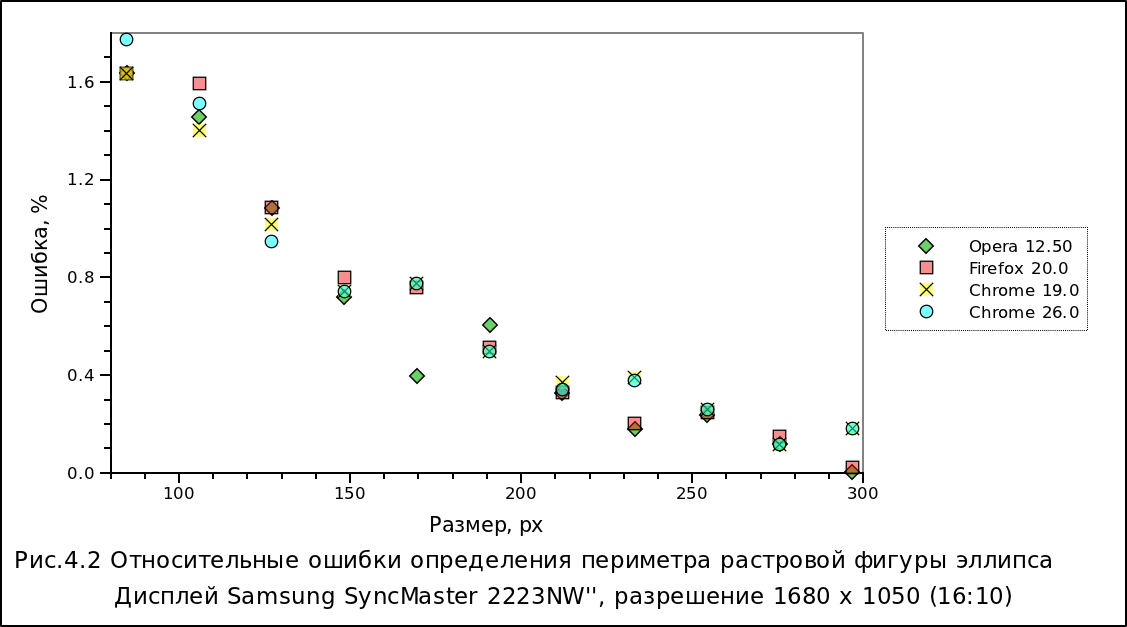
На основании этих экспериментов можно сделать вывод, что размеры изображения для измерения площади долны быть около 270 пикселей. Изображения больших размеров не следует делать в целях экономии места базы данных, предназначенной для хранения изображений.
При этом уровень ошибок, показанных на рис.4.1 и 4.2 соответствуют 100%-ному масштабу изображения. При изменении масштаба (zoom, зуммировании) уровень ошибок колеблется, но ход ошибок аналогичен показанному на рисунках. Причина таких колебаний понятна - из-за изменений размера виртуального пиксела при изменении масштаба изображения [17,18]. Более точные результаты получаются при совпадении физического и виртуального пикселей, то есть, когда совпадает разрешение монитора и разрешение изображения. Менее точные, - когда на виртуальный пиксел приходится не целое число физических пикселей. Поэтому на втором и третьем этапах лучше проводить расчёты площади и периметра без масштабирования (зуммирования) изображения.
Последнее правило легко соблюдать для десктопов. Как показали эксперименты, для планшетов и мобильных устройств с маленькими экранами использование нашего примера также возможно, но требуется доработка по автоматизации изменения масштаба изображения в зависимости от характеристик дисплея [18]).
Третий этап нашего примера можно использовать для исследования влияния ошибок измерения ширины и высоты эллипса. Изображение заданных размеров, также, как и на втором этапе, копируется из первого холста. Кроме этого, задаются размеры фигуры в миллиметрах и ошибка измерения. Вычисляются три типа ошибок вычисления площади и периметра: 1) за счёт ошибок измерения линейных размеров; 2) за счёт ошибок представления фигуры в виде растрового изображения; 3) суммарные ошибки.
Учитывая, что при измерении размеров раковин имеется возможность использовать штангенциркули, имеющие различные точности измерений (0.1, 0.05 и 0.02 мм), можно рассчитать относительную точность расчёта площади и периметра. На рис.5.1 и рис.5.2 представлены результаты таких расчётов.


В предыдущем разделе было показано, что изображения со средними размерами в 270 пикселей являются оптимальными для нашей задачи. Для изображений такого размера относительные ошибки определения площади равны примерно 0.3% для площади и 0.2% для периметра. Поэтому можно потребовать, чтобы ошибки площади и периметра за счёт ошибок измерения не превышали соответственно 0.3% и 0.2%. На рис.5.1 и 5.2 видно, что эти условия выполняются при следующих соотношениях размеров фигур и точности измерений:
Эти условия можно рекомендовать при проведении измерений размеров раковины.
При выполнении измерений с рекомендуемой точностью для изображений с размерами 270 и более пикселей суммарные относительные ошибки расчёта площади и периметра не должны превышать соответственно 0.6% и 0.4%. При желании, проверку выполнения полученных нами результатов можно сделать с помощью этапа 3 веб-инструмента.
Проверку выводов предыдущих разделов доклада можно выполнить, используя четвёртый этап нашего примера на снимках и по результатам измерений раковин мидий из базы данных, наполняемой в настоящее время студентами группы МК-5 в рамках некоторых курсовых работ.
В дополнение к линейным размерам обмерялись также периметры контуров изображений, которые использовались в качестве тестовых значений. Расхождения между вычисляемыми и тестовыми значениями периметров не превышают точности обмеров периметра.
Расчёт ошибок можно осуществить, используя четвёртый, первый и третий этапы в предлагаемой ниже последовательности действий на примере одного тестового снимка раковины.

Рис.6.1 Пример изображения раковины, помещённого на холст с помощью кнопки "Загрузка".
Одновременно с изображением загружаются значения измерений ширины и высоты, полученные при обмерах раковины штангенциркулем, а также инструментальная погрешность используемого штангенциркуля.
Нажимая на кнопку "Расчёты" этой же формы получаем результаты расчётов площади и периметра, показанные на рис.6.2.

Рис.6.2 Пример изображения раковины с выделенным контуром и предварительных результатов, получаемых с помощью кнопки "Расчёты".
Как видно из рисунка, определяются пока что только лишь погрешности (косвенные погрешности) определения площади и периметра за счёт инструментальных погрешностей определения ширины и высоты (прямые погрешности). Погрешности за счёт разрешения снимка, приближения растром, и, соответственно, суммарные ошибки, ещё не определяются.
Но, поскольку теперь нам известны размеры изображения в пикселах и миллиметрах, мы можем определить незвестные погрешности с помощью первого и третьего этапов нашего примера. При этом предполагается, что погрешности для эллипса с шириной и высотой раковины, будут равны погрешностям для самой раковины. При этом исходим из того факта, что форма эллипса, её площадь и периметр примерно равны аналогичным характеристикам раковины и алгоритмы их выделения и определения одни и те же.
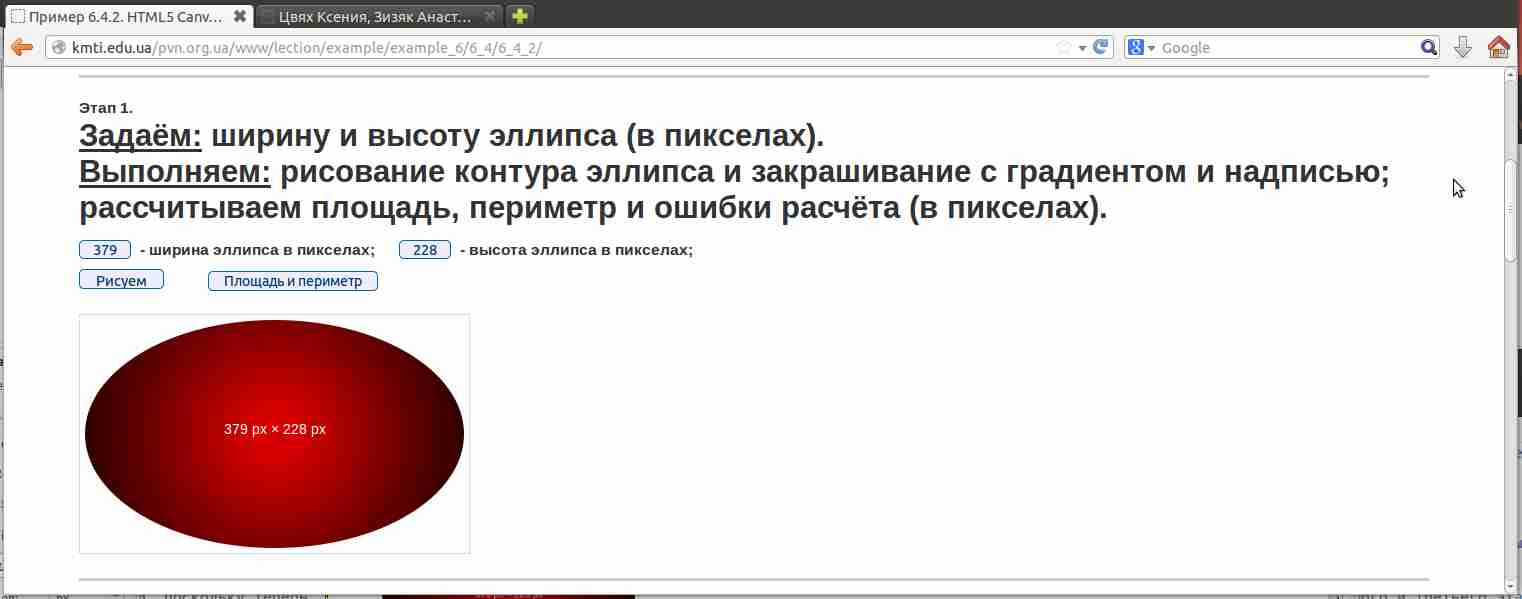
Рис.6.3 Пример эллипса, получаемого с помощью кнопки "Рисуем", с разрешением, эквивалентным разрешению снимка раковины.
Для нас сейчас задача этого этапа - только лишь рисование эллипса, а расчёты площади, периметра и погрешностей выполним далее, используя третий этап.

Рис.6.4 Пример изображения эллипса с выделенным контуром и результатов, получаемых с помощью кнопки "Площадь и периметр".
Следует учитывать, что погрешность (ошибка) на этом этапе задаётся числом 0.02, как это обычно пишется в паспорте штангенциркуля, а на этапе 4 мы видим эту погрешность как ±0.01 (в таком виде она вводится в базу данных при обмерах раковины.
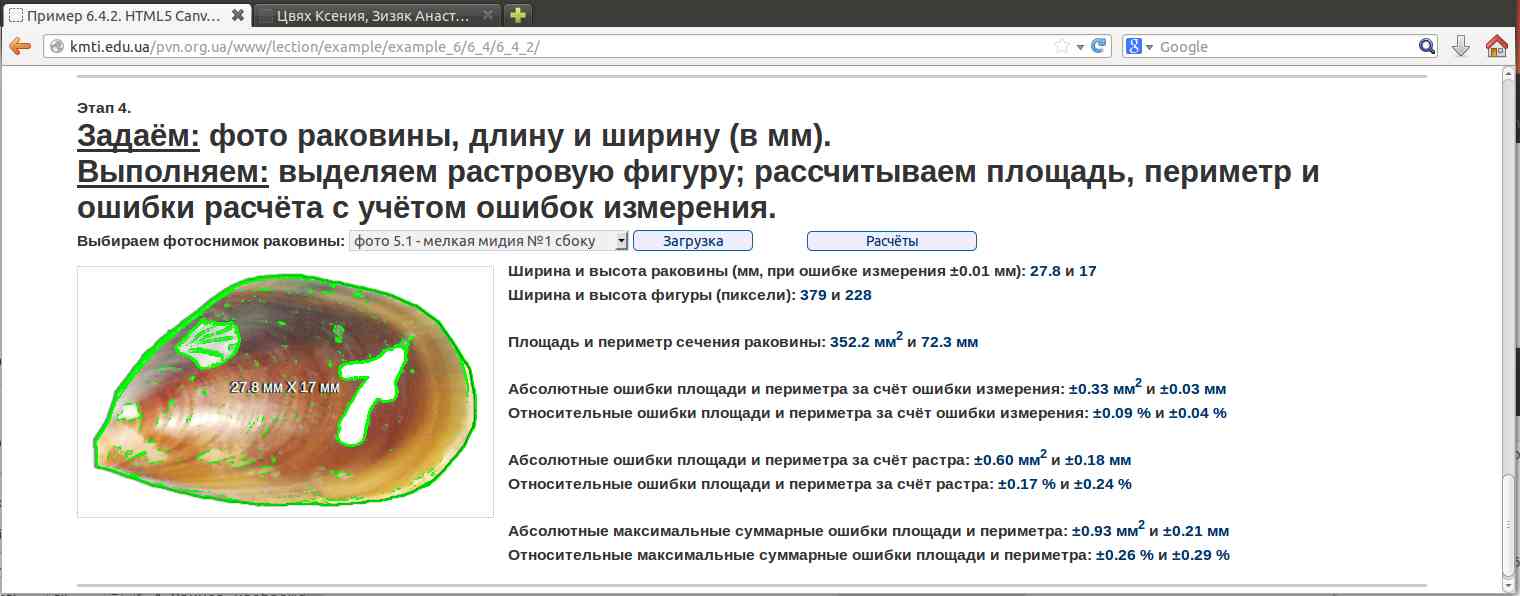
Рис.6.5 Пример изображения раковины с выделенным контуром и окончательных результатов, полученных с помощью кнопки "Расчёты".
В результате проделанной работы:
В заключение необходимо сказать, что выполненная работа является одним из этапов недавно задуманного с нашим участием проекта "Мидия", предназначенного для накопления данных о черноморской мидии и последующих морфометрических измерений с помощью средств манипуляции 2D- и 3D-изображениями, предусмотренных стандартами консорциума W3C и в рамках подхода WEB2.0
Canvas (русс. - холст) встраивается в HTML-документ с помощью тэга <canvas>...</canvas>
К этому тэгу, как и к другим тэгам, можно обращаться из скриптов, как к объекту доменной модели или по имени. Все свойства и методы API содержатся в так называемых контекстах - объектах, посвящённых какому-то типу графики. Мы будем использовать контекст для работы с 2D-изображениями. Этого достаточно, хотя эти и другие, более развитые методы, имеются в контексте для работы с 3D.
Итак, встраиваем элемент Canvas в HTML-документ и получаем его в скрипте, как объект. Затем получаем 2D-контекст для этого объекта:Координаты холста отсчитываются от точки x=0, y=0, находящейся в левом верхнем углу (начало координат или начало отсчёта). Координаты увеличиваются в горизонтальном направлении вправо и в вертикальном - вниз. Каждая координата обозначает местонахождение соответствующего пиксела.
Обо всех свойствах и методах API HTML5 Canvas и примерах их применения можно узнать в многочисленных источниках, например, здесь [1,2,3]. Ниже кратко рассмотриваются лишь свойства и методы API HTML5 Canvas, используемые в наастоящем примере.
Для построения эллипса используется метод преобразования окружности, который должен быть известен вам из школьной геометрии.
Для копирования изображения из одного холста на другой можно использовать новую возможность HTML5 - поддержка интернет-адресов (или путей к файлу) типа dataURL (URL с данными-закодированными изображениями). То есть, такие адреса содержат не только пути (ссылки) к изображению, но сами изображения в закодированном виде (обычно используется Base64). Поэтому мы имеем возможность превратить содержимое холста в такой адрес с изображением (метод toDataURL("MIME-тип_изображения")), не сохраняя его на внешний носитель, загрузить его в объект-изображение, не отображая это изображение, и затем загрузить и отобразить на холсте (метод drawImage(адрес_изображения, 0, 0)). Такую последовательность действий можно осуществить с помощью операторов:
var srcImg = cnvs_in.toDataURL("image/png"); // Создаём dataURL, взяв изображение из первого холста
var img_ellips = new Image(); // Создаём элемент Image
img_ellips.src = srcImg; // и передаём ему путь к dataURL
img_ellips.onload = function() {
cntxt_out.drawImage(img_ellips, 0, 0); // Загружаем объект-изображение на нужный холст
}